N-Dimensional Optimal Filter (NDOF)¶
Motivation¶
The idea here is that a signal may be a linear superposition of two different pulses each with different time constants. In this case we can't use a single template OF to extract the right parameters (amplitude of templates and offset time). The cartoon below shows this.
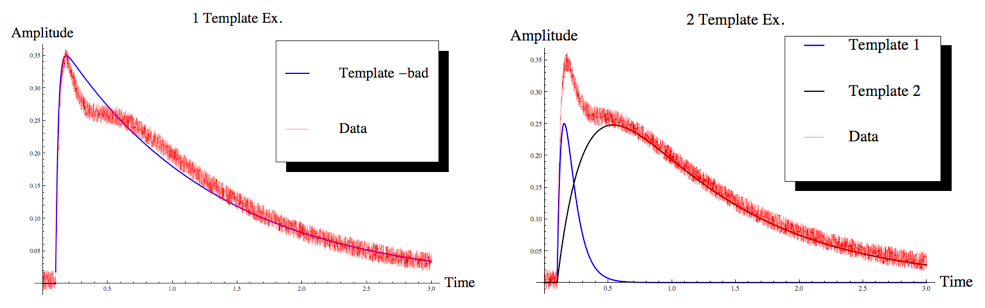
This OF is intended for Phonon pulses, whose shape carry position dependence.
Theory¶
For such a case we model our signal as a linear superposition of N templates \{A^{k}|k=1,2\cdots N\} with a noise i.e. S(t)=a_{1}A^{k}(t)+a_{2}A^{2}(k)+ \cdots +n(t). Following this, we design a frequency domain \chi^{2}. This generalized discriminant is given as:
\chi^{2}(\vec{a},t_{0})=\sum_{\nu}\frac{|\tilde{S}(\nu)-e^{-i2\pi\nu t_{0}}a^{j}\tilde{A}_{j}(\nu)|^{2}}{\tilde{J}(\nu)}
Here, J(\nu) is the Power Spectral density in frequency in Fourier or frequency space. It is calculated from noise traces as described in Chapter 1. Also the offset time t_{0} is encoded as a phase, and the set of all N template amplitude parameters {a}, is written as a N-Dimensional vector (hence the name ND). The sum over templates is written in Einstein notation for brevity.
In this formulation the \chi^{2} has N+1 d.o.f, the +1 coming from t_{0}. We want to minimize the \chi^{2} w.r.t to all N+1 parameters. However, we have N linear equations coming from \partial\chi^{2}/\partial a^{k}=0 \forall k. The t_{0} dependence is extremely nonlinear. So we formulate the best fit parameters as a function of t_{0},
\vec{a}(t_{0})=\boldsymbol{P^{-1}}\cdot \vec{q}(t_{0})
\boldsymbol{P_{kj}}\equiv\sum_{\nu}\frac{\tilde{A}_{k}^{\ast}(\nu)\tilde{A}_{j}(\nu)}{\tilde{J}(\nu)}
q_{k}(t_{0})\equiv\sum_{\nu}\frac{\tilde{A}_{k}^{\ast}(\nu)\tilde{S}(\nu)e^{i2\pi\nu t_{0}}}{\tilde{J}(\nu)}
and hence the \chi^{2} as a function of t_{0}:
\chi^{2}(t_{0})=\sum_{\nu}\frac{1}{\tilde{J}(\nu)}\big(\tilde{S}^{\ast}(\nu)\tilde{S}(\nu)-[\boldsymbol{P^{-1}}\cdot \vec{q}(t_{0})]^{j}\tilde{A}_{j}^{\ast}(\nu)\tilde{A}_{k}(\nu)[\boldsymbol{P^{-1}}\cdot \vec{q}(t_{0})]^{k}
The best t_{0} can thus be found from numerically by looking for the minima of \chi^{2}(t_{0}).
The full derivation can be found in the note from the Reference section below, particularly Sec. 3.