Above plots: gif / eps / pdf /
(home , top , next, previous )
| b hadron species | average lifetime | average lifetime relative to B0 average lifetime |
| B0 | 1.519 ± 0.007 ps | |
| B+ | 1.641 ± 0.008 ps | 1.079 ± 0.007 |
| Bs | 1.516 ± 0.011 ps | 0.998 ± 0.009 |
| Bc | 0.452 ± 0.033 ps | |
| Λb | 1.429 ± 0.024 ps | 0.941 ± 0.016 |
| Ξb− | 1.56 +0.27 −0.25 ps | |
| Ωb− | 1.13 +0.53 −0.40 ps | |
| Ξb−, Ξb0 mixture | 1.49 +0.19 −0.18 ps | |
| b-baryon mixture | 1.402 ± 0.023 ps | 0.923 ± 0.016 |
| b-hadron mixture | 1.568 ± 0.009 ps |
The table below gives other Bs lifetime averages, consisting of different mixtures of the two Bs mass eigenstates. The "Bs → flavour specific" lifetime is measured mainly with Bs → Ds lepton X decays; it is used as input to extract the long and short lifetimes of the Bs system (see next section). The "Bs → Ds X" lifetime is ill-defined because it includes an unknown proportion of short and long components. The "Bs → J/ψ φ" lifetime is an average of the results from single exponential fits. Nowadays, the time dependence and the angular dependence of the Bs → J/ψ φ decays is analysed in a more sophisticated way in order to extract separately the long and short lifetimes (see further below).
| mixture of the two Bs mass eigenstates | average lifetime |
| Bs → flavour specific | 1.463 ± 0.032 ps |
| Bs → Ds X | 1.466 ± 0.031 ps |
| Bs → J/ψ φ | 1.429 ± 0.088 ps |
Combined result on the relative decay width difference in the B0 system:
| s×ΔΓd/Γd = 0.015 ± 0.018 | from Belle, BABAR and DELPHI |
The quantity s = sign(Re(λCP)), where λCP = (q/p)×ACP/ACP refers to a CP-even final state (e.g. J/ψKL), is predicted to be equal to s= +1 to a high degree of confidence from the Standard Model fits to all available constraints on the unitarity triangle.
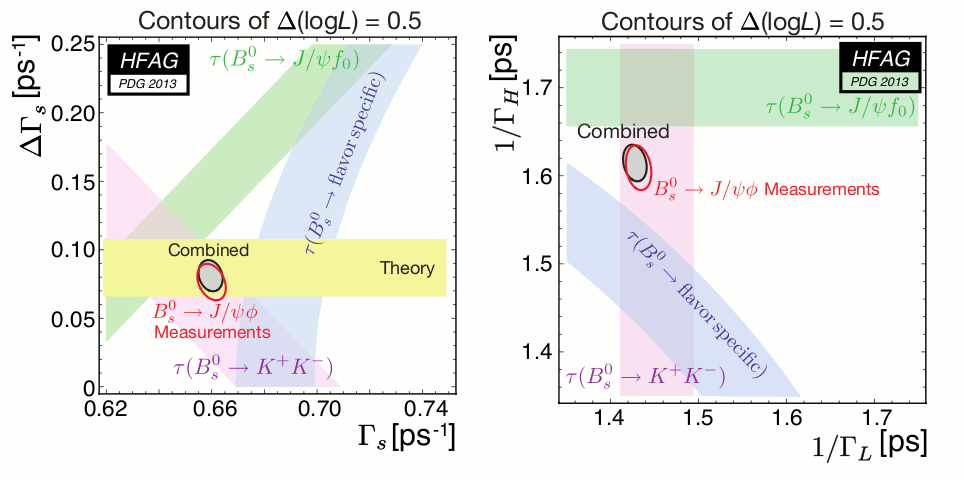
The ATLAS, CDF, D0 and LHCb analyses of the Bs → J/ψ φ decay provide information on Γs, ΔΓs and the weak phase φsccs, defined as the phase difference between the mixing amplitude and the b→ccs decay amplitude of the Bs meson. Combined values of the average decay width Γs and the decay width difference ΔΓs are obtained from of a two-dimensional fit of the experimental results. In this fit, the CP-violating phase φsccs is fixed to +0.04 , which is the central value of the φsccsaverage described below. The correlation between Γs and ΔΓs in each analysis is taken into account (but correlations with other parameters are ignored). The following additional constraints are applied, using effective lifetime measurements:
| Fit results from ATLAS, CDF, D0 and LHCb data |
without constraint from effective lifetime measurements |
with constraints I and II |
with constraints I, II and III |
| Γs | 0.6600 ± 0.0054 ps | 0.6557 ± 0.0049 ps | 0.6596 ± 0.0046 ps |
| 1/Γs | 1.515 ± 0.012 ps | 1.525 ± 0.011 ps | 1.516 ± 0.011 ps |
| τShort = 1/ΓL | 1.432 ± 0.015 ps | 1.432 ± 0.014 ps | 1.428 ± 0.013 ps |
| τLong = 1/ΓH | 1.609 ± 0.025 ps | 1.622 ± 0.023 ps | 1.615 ± 0.021 ps |
| ΔΓs | +0.077 ± 0.013 ps−1 | +0.086 ± 0.012 ps−1 | +0.081 ± 0.011 ps−1 |
| ΔΓs/Γs | +0.116 ± 0.020 | +0.131 ± 0.018 | +0.123 ± 0.017 |
| correlation ρ(Γs, ΔΓs) | −0.324 | −0.245 | −0.195 |

Above plots: gif /
eps /
pdf /
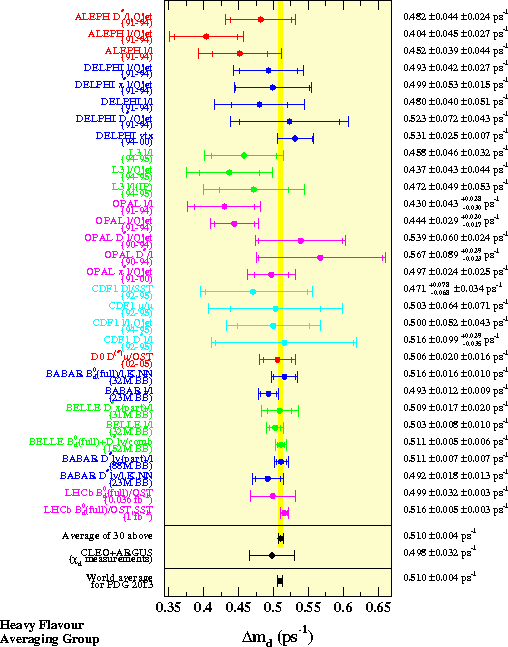
| Δmd = 0.510 ± 0.004 ps−1 | from time-dependent measurements at ALEPH, DELPHI, L3, OPAL, CDF, D0, BABAR, BELLE, LHCb |
| χd = 0.182 ± 0.015 | from time-integrated measurements at ARGUS and CLEO |
Assuming no CP violation in the mixing and no width difference in the B0 system, and assuming a B0 lifetime of 1.519 ± 0.007 ps (the experimental average listed above), all above measurements can be combined to yield the following world averages:
| Δmd =
0.510
±
0.004
ps−1
xd = 0.775 ± 0.006 χd = 0.1875 ± 0.0020 |
from all ALEPH, DELPHI, L3, OPAL, CDF, D0, BABAR, BELLE, LHCb, ARGUS and CLEO measurements |
In the plot below, all individual measurements are listed as quoted by the experiments; they might assume different physics inputs. The averages (which take into account all known correlations) are quoted after adjusting all the individual measurements to the common set of physics inputs. The χd average from ARGUS and CLEO is converted to a Δmd measurement assuming no CP violation, no width difference in the B0 system and a B0 lifetime of 1.519 ± 0.007 ps.
colour gif /
colour eps /
black-and-white eps /
Same without average including time-integrated (χd) measurements:
colour eps /
black-and-white eps /
Only measurements and average at LEP and CDF1:
colour eps /
black-and-white eps /
Only measurements and average at LEP:
colour eps /
black-and-white eps /
Only measurements and average at asymmetric B factories:
colour eps /
black-and-white eps /
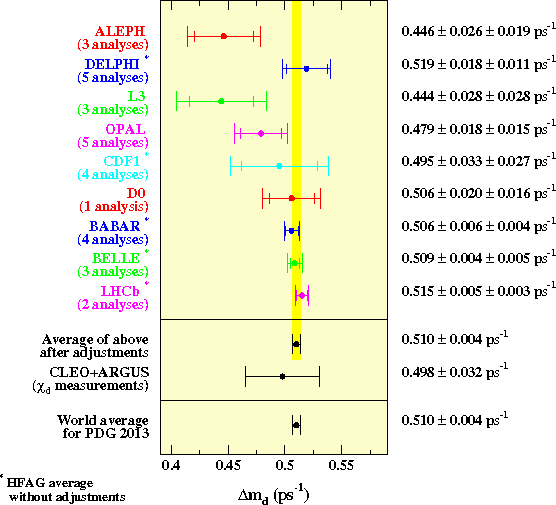
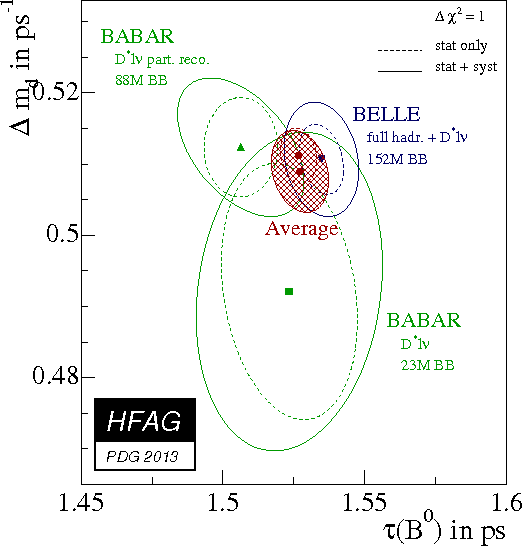
In the plot below,
all individual experiment averages are listed as quoted by the experiments
(or computed by the working group without performing any adjustments);
they might assume different physics inputs. The global averages are quoted
after adjusting all the individual measurements to the common set of physics
inputs. The χd average from ARGUS and CLEO is converted to a Δmd measurement
assuming no CP violation, no width difference in the B0 system and a
B0 lifetime of
1.519
±
0.007
ps.
colour gif /
colour eps /
black-and-white eps /
colour gif /
colour eps /
| Δms = 17.69 ± 0.08 ps−1 | CDF, LHCb |
With a mean B0s lifetime of 1/Γs = 1.516 ± 0.011 ps, a decay width difference of ΔΓs = +0.081 ± 0.011 ps−1 and the assumption of no CP violation in B0s mixing, this leads to
| xs = 26.82 ± 0.23 |
| χs = 0.499309 ± 0.000012 |
The parameters |q/p|, ASL and Re(εB)/(1+|εB|2) are thus equivalent. There is CP violation in the mixing if |q/p| is different from 1, i.e. ASL is different from 0.
Averages are given below separately for the B0 and the Bs systems. Two sets of averages are given for the B0 system in the first table: a first set using only measurements performed at Υ(4S) machines, and a second set using all measurements (excluding those that assume no CP violation in Bs mixing). The second table presents an average for the Bs system. Measurements performed at high energy that do not separate the B0 and Bs contributions are no longer used to obtain the final averages (at this time, the only measurements at high energy used in the averages are from D0).
| CP violation parameter in B0 mixing | |
|
|q/p| =
1.0002
±
0.0028
ASL = −0.0005 ± 0.0056 Re(εB)/(1+|εB|2) = −0.0001 ± 0.0014 |
from measurements at the Υ(4S) |
|
|q/p| =
0.9997
±
0.0013
ASL = +0.0007 ± 0.0027 Re(εB)/(1+|εB|2) = +0.0002 ± 0.0007 |
world average |
| CP violation parameter in Bs mixing | |
|
|q/p| =
1.0086
±
0.0028
ASL = −0.0171 ± 0.0055 |
world average |
The above world averages ASL(B0) = +0.0007 ± 0.0027 and ASL(Bs) = −0.0171 ± 0.0055 are obtained from a two-dimensional fit of the CLEO, BABAR, Belle and D0 results: the correlation coefficient between them is found to be −0.462 .
| Combined result from CDF, D0, ATLAS and LHCb data |
|
| φsccs | +0.04 +0.10 −0.13 |
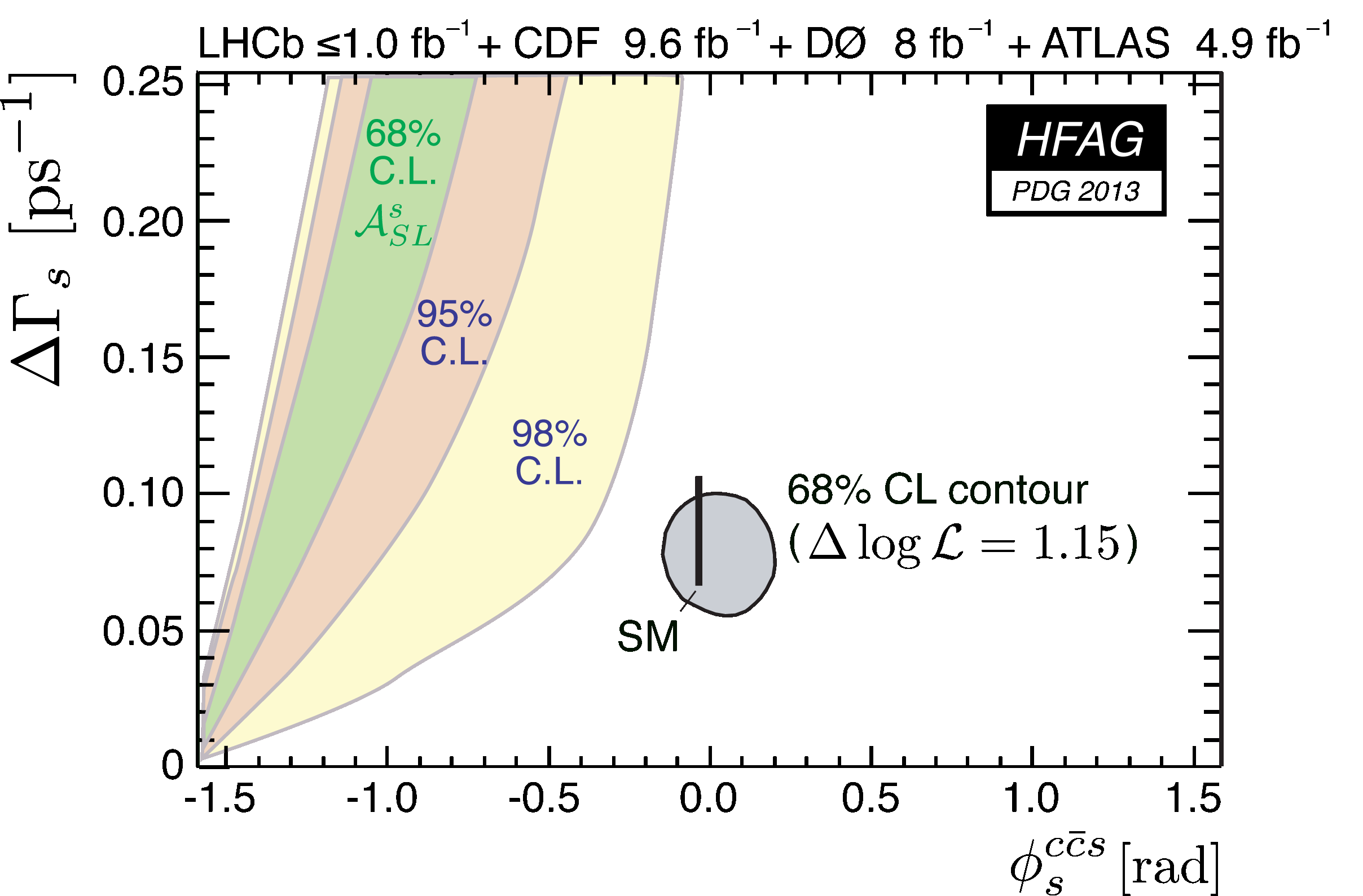
The two plots below show different 68% confidence-level contours in the (φsccs, ΔΓs) plane. The left plot shows the individual contours of CDF, D0 and LHCb, their combined contour (solid line and shaded area), as well as the Standard Model predictions. The prediction for φsccs is taken as the indirect determination of −2βs via a global fit to experimental data within the Standard Model, −2βs = −0.0363+0.0016−0.0015 [CKMfitter, Phys. Rev. D84, 033005 (2011)] , while the Standard Model prediction for ΔΓs is 0.087 ±0.021 ps−1 [A. Lenz and U. Nierste, arXiv:1102.4274 [hep-ph]]. The combined result is consistent with these predictions at the 0.56 σ level. The right plot shows the same combined contour and SM predictions together with the regions allowed at 68% and 95% CL by the average measurements ASL(Bs) = −0.0171 ± 0.0055 and Δms = 17.69 ± 0.08 ps−1, through the relation tanφ12 = ASL(Bs) × Δms / ΔΓs, where φ12 = arg(−M12/Γ12) is the phase mismatch between the off-diagonal elements of the mass and decay matrices of the Bs−Bs system. This region is drawn under the assumption that possible new physics will not affect the phase difference φsccs−φ12, i.e. that this phase difference is equal to its Standard Model prediction [A. Lenz and U. Nierste, arXiv:1102.4274 [hep-ph]].
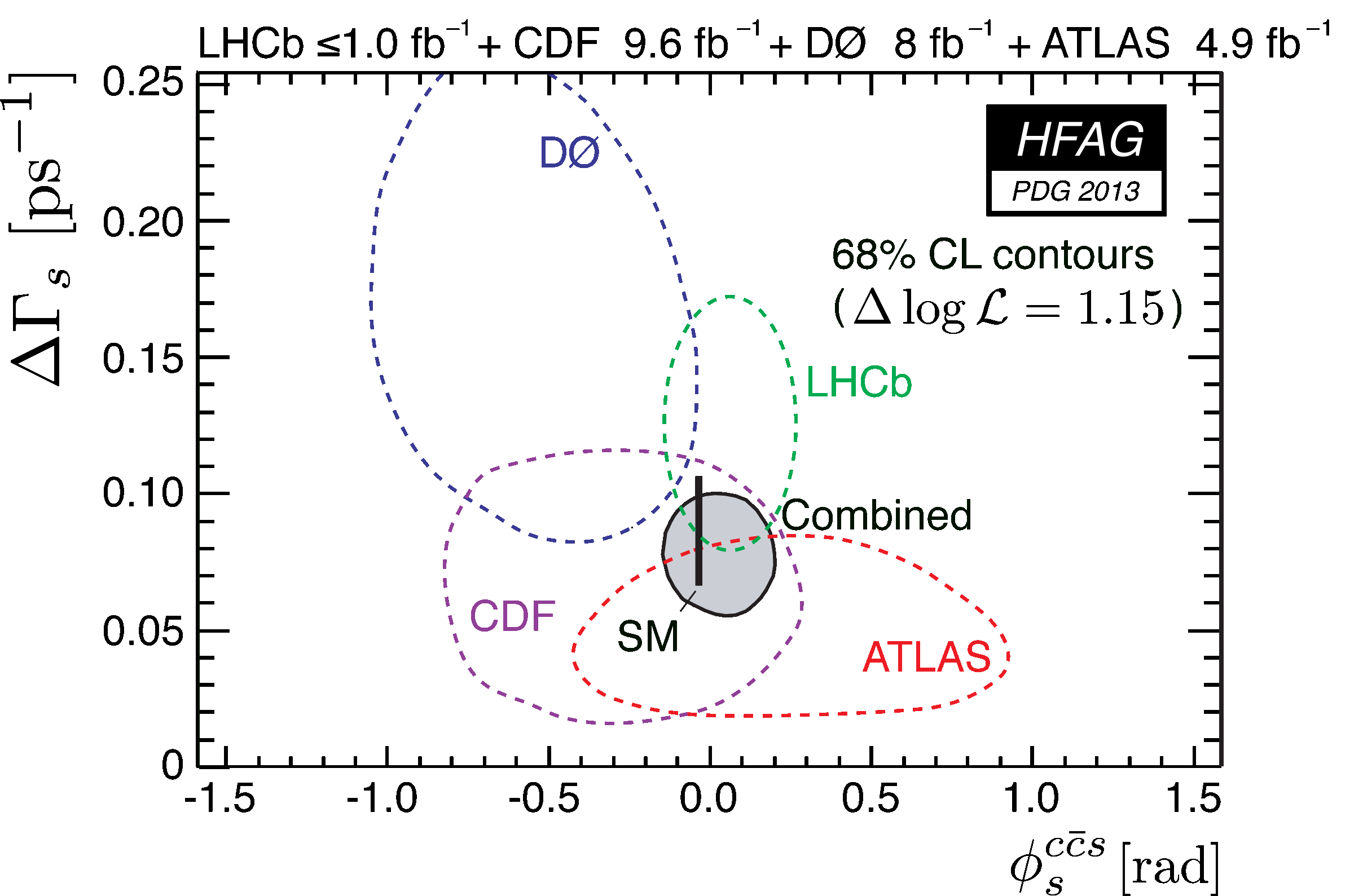
ATLAS, CDF, D0, LHCb, and their average: colour gif /
colour eps /
colour pdf /
average and region allowed by ASL(Bs): colour gif /
colour eps /
colour pdf /
| f+−/f00 = 1.056 ± 0.028 | from ratios of reconstructed B+ and B0 mesons
at BABAR, BELLE and CLEO
(assumptions made, see text above) |
| f00 = 0.487 ± 0.013 | from absolute measurement of
B0 mesons at BABAR
(no assumptions) |
Assuming f+− + f00 = 1, the above two independent results
(which are consistent with each other)
can be combined to yield:
| b hadron species | fraction in Υ(4S) decay | ratio |
| B+ B− | f+− = 0.513 ± 0.006 | f+−/f00 = 1.055 ± 0.025 |
| B0 anti-B0 | f00 = 0.487 ± 0.006 |
| final states | fraction in Υ(5S) decay | ratio of fractions |
| Bu,d(*) anti-Bu,d(*)(π(π)) | fu,d(Υ(5S)) = 0.759 +0.027 −0.040 | |
| Bs(*) anti-Bs(*) | fs(Υ(5S)) = 0.199 ± 0.030 | fs(Υ(5S))/fu,d(Υ(5S)) = 0.262 +0.051 −0.043 |
| no open bottomness | fnoB(Υ(5S)) = 0.042 +0.046 −0.006 |
The plot below shows the published measurements of fs.
All values have been obtained assuming fnoB=0.
They are quoted as in the original publication,
except for the most recent measurement of Belle which
is quoted as fs = 1-fud. The average value of
all these measurements is quoted with or without the assumption that
fnoB=0,
after performing adjustments
to common external inputs.
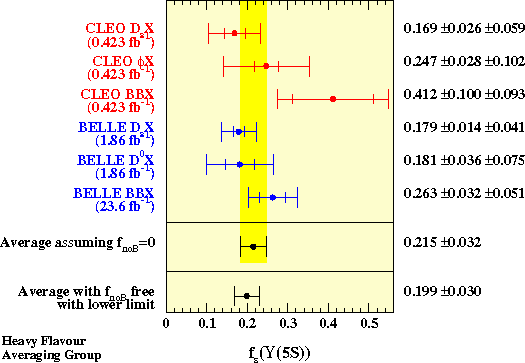
| b hadron species | fraction in Z decays | correlation with f(Bs) | correlation with f(b-baryon) |
| Bs | f(Bs) = 0.103 ± 0.009 | ||
| b baryons | f(b-baryon) = 0.090 ± 0.015 | +0.043 | |
| B0 or B+ | f(Bd) = f(Bu) = 0.404 ± 0.009 | −0.527 | −0.872 |
| Bs / (B0 or B+) ratio | f(Bs)/f(Bd) = 0.254 ± 0.025 |
| χbar(LEP) = 0.1259 ± 0.0042 | LEP average from LEP EW WG |
| b hadron species | fraction in p-pbar collisions at 1.8−2 TeV | correlation with f(Bs) | correlation with f(b-baryon) |
| Bs | f(Bs) = 0.111 ± 0.014 | ||
| b baryons | f(b-baryon) = 0.212 ± 0.069 | −0.581 | |
| B0 or B+ | f(Bd) = f(Bu) = 0.338 ± 0.031 | +0.425 | −0.984 |
| Bs / (B0 or B+) ratio | f(Bs)/f(Bd) = 0.328 ± 0.039 |
| χbar(Tevatron) = 0.147 ± 0.011 | average of CDF and D0 measurements |
| b hadron species | fraction at high energy | correlation with f(Bs) | correlation with f(b-baryon) |
| Bs | f(Bs) = 0.104 ± 0.006 | ||
| b baryons | f(b-baryon) = 0.093 ± 0.015 | −0.277 | |
| B0 or B+ | f(Bd) = f(Bu) = 0.402 ± 0.007 | −0.112 | −0.924 |
| Bs / (B0 or B+) ratio | f(Bs)/f(Bd) = 0.258 ± 0.016 |
| χbar = 0.1259 ± 0.0042 | LEP average from LEP EW WG |
| χbar = 0.147 ± 0.011 | Tevatron average |
| χbar = 0.1284 ± 0.0069 | weighted average of above two, with error rescaled by factor 1.8 according to PDG prescription |
Note: