People working on this:
Marco Gersabeck
Notation:
This combination uses measurements of direct and indirect CP violation
to extract the level of agreement for a no-CP-violation hypothesis.
The observables are:
Year
Experiment
Results
Δ〈t〉/τ
〈t〉/τ
Comment
Reference
2012
Belle preliminary
AΓ = (−0.03 ±0.20 (stat.) ±0.08 (syst.))%
-
-
976 fb−1 near Υ(4S) resonance
M. Staric for the Belle Collab., arXiv:1212.3478.
2012
BaBar
AΓ = (0.09 ±0.26 (stat.) ±0.06 (syst.))%
-
-
468 fb−1 near Υ(4S) resonance
J.P. Lees et al. (BaBar Collab.), Phys.Rev. D87 (2013) 012004.
2011
LHCb
AΓ = (−0.59 ±0.59 (stat.) ±0.21 (syst.))%
-
-
28 pb−1 √ s = 7 TeV pp collisions
R. Aaij et al. (LHCb Collab.), JHEP 1204 (2012) 129.
2008
BaBar
ACP(KK) = (0.00 ±0.34 (stat.) ±0.13 (syst.))%
ACP(ππ) = (−0.24 ±0.52 (stat.) ±0.22 (syst.))%
0.00
1.00
385.8 fb−1 near Υ(4S) resonance
B. Aubert et al. (BABAR Collab.), Phys. Rev. Lett. 100, 061803 (2008).
2012
Belle preliminary
ΔACP = (−0.87 ±0.41 (stat.) ±0.06 (syst.))%
0.00
1.00
976 fb−1 near Υ(4S) resonance
B.R. Ko for the Belle Collab., arXiv:1212.1975.
2012
CDF
ΔACP = (−0.62 ±0.21 (stat.) ±0.10 (syst.))%
0.25
2.58
9.7 fb−1
√ s =
1.96 TeV p p collisions
T. Aaltonen et al. (CDF Collab.), Phys.Rev.Lett. 109 (2012) 111801.
2013
LHCb preliminary
ΔACP = (−0.34 ±0.15 (stat.) ±0.10 (syst.))%
0.11
2.10
1.0 fb−1 √ s = 7 TeV pp collisions, prompt D*
The LHCb Collaboration, LHCb-CONF-2013-003.
2013
LHCb
ΔACP = (0.49 ±0.30 (stat.) ±0.14 (syst.))%
0.02
1.06
1.0 fb−1 √ s = 7 TeV pp collisions, B→D0μX
R. Aaij et al. (LHCb Collab.), arXiv:1303.2614.
Fit Result
Agreement with no CP violation
CL = 2.1x10−2
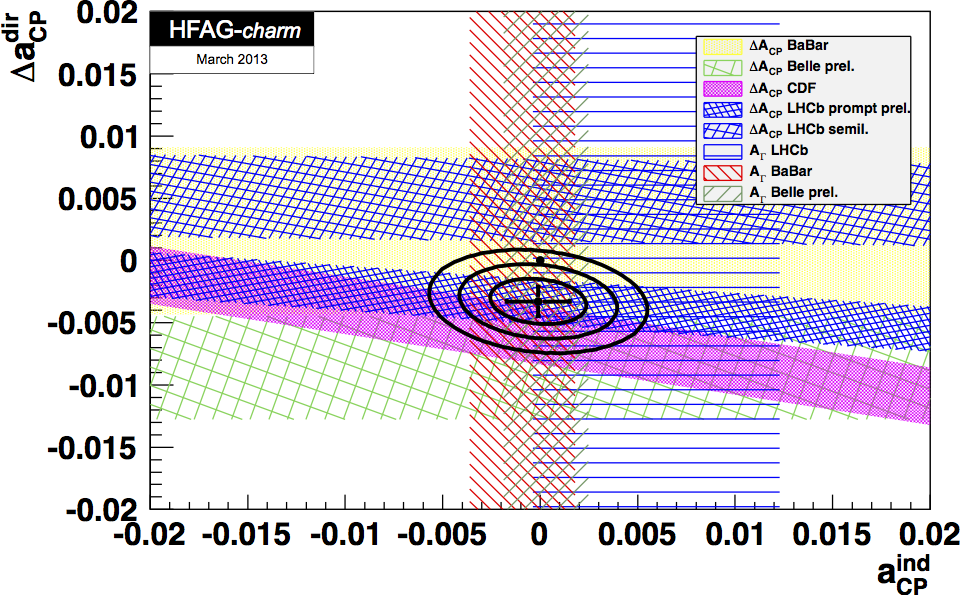
Combination Plot: The combination plot shows the measurements listed in the Table above for ΔACP and AΓ, where the bands represent ±1σ intervals. The point of no CP violation (0,0) is shown as a filled circle, and two-dimensional 68% CL, 95% CL, and 99.7% CL regions are plotted as ellipses with the best fit value as a cross indicating the one-dimensional uncertainties in their center.

From the fit, the change in χ2 from the minimum value for the no-CPV point (0,0) is 7.7; this corresponds to a CL of 2.1x10−2 for two degrees of freedom. Thus the data is consistent with no CP violation at 2.1% CL. The central values and ± 1σ errors for the individual parameters are: