
 |
| Time-Dependent CP Asymmetries in Bd → D+–π–+, etc. (sin(2β+γ)/sin(2φ1+φ3)) |
| GLW and ADS Analyses of B– → D(*)K(*)– (γ/φ3) |
| Dalitz Plot Analysis of B– → D(*)K(*)– with D → KSπ+π–, ... (γ/φ3) |
| Parameter | Value | Ref. / Comments |
|---|---|---|
| τ(Bd) | (1.536 ± 0.014) ps | HFAG - Oscillations/Lifetime (Winter 2004) |
| Δmd | (0.502 ± 0.007) ps–1 | HFAG - Oscillations/Lifetime (Winter 2004) |
|
|A⊥|2 (CP-odd fraction in B0→ J/ψK* CP sample) |
0.245 ± 0.015 ± 0.004 (note: acceptance-corrected central value; the uncorrected value is: 0.230) |
BABAR-CONF-04/38, hep-ex/0408127 |
| 0.181 ± 0.012 ± 0.008 | Belle-CONF-0438, hep-ex/0408104 | |
| 0.211 ± 0.011 | Average (CL = 0.0025 → 3.0σ) |
| Parameter: sin(2β)/sin(2φ1) (if β/φ1 dominant weak phase) | ||||
|---|---|---|---|---|
| Mode | BABAR | Belle | Average | Ref. / Comments |
| Charmonium: | N(BB)=227m | N(BB)=152m | - | BABAR-CONF-04/38, hep-ex/0408127 (submitted to PRL) Belle-Preprint-2004-31, hep-ex/0408111 (submitted to PRD) |
| J/ψKS, ψ(2S)KS, χc1KS, ηCKS | 0.75 ± 0.04stat | 0.73 ± 0.06stat | ||
| J/ψKL (ηCP=+1) | 0.57 ± 0.09stat | 0.77 ± 0.13stat | ||
| J/ψK*0 (K*0 → KSπ0) | 0.96 ± 0.32stat | 0.10 ± 0.45stat | ||
| All charmonium | 0.722 ± 0.040 ± 0.023 | 0.728 ± 0.056 ± 0.023 |
0.725 ± 0.037 (0.033stat-only) |
CL = 0.91 |
| s-penguin: | N(BB)=209-227m | N(BB)=274m | ||
| φK0 | 0.50 ± 0.25 +0.07–0.04 | 0.06 ± 0.33 ± 0.09 | 0.34 ± 0.20 CL=0.30 |
BABAR-CONF-04/033, hep-ex/0408072 Belle-CONF-0435, hep-ex/0409049 |
| η'KS | 0.27 ± 0.14 ± 0.03 | 0.65 ± 0.18 ± 0.04 | 0.41 ± 0.11 CL=0.10 (1.6σ) |
BABAR-CONF-04/040, hep-ex/0408090 Belle-CONF-0435, hep-ex/0409049 |
| f0KS | 0.95 +0.23–0.32 ± 0.10 | –0.47 ± 0.41 ± 0.08 | 0.39 ± 0.26 CL=0.008 (2.7σ) |
BABAR-CONF-04/019, hep-ex/0408095 Belle-CONF-0435, hep-ex/0409049 |
| π0KS | 0.35 +0.30–0.33 ± 0.04 | 0.30 ± 0.59 ± 0.11 | 0.34 +0.27–0.29 CL=0.94 |
BABAR-CONF-04/030, hep-ex/0408062 Belle-CONF-0435, hep-ex/0409049 |
| ωKS | not yet available | 0.75 ± 0.64 +0.13–0.16 | 0.75 ± 0.64 +0.13–0.16 | Belle-CONF-0435, hep-ex/0409049 |
|
K+K–KS (excluding φKS) |
0.55 ± 0.22 ± 0.04 ± 0.11CP-even (fCP-even= 0.89 ± 0.08 ± 0.06 [moments]) |
0.49 ± 0.18 ± 0.04 +0.17–0.00CP-even (fCP-even= 1.03 ± 0.15 ± 0.05 [SU(2)]) |
0.53 ± 0.17 CL=0.72 (rescaled to average fCP-even= 0.93 ± 0.09) |
BABAR-CONF-04/025, hep-ex/0408076 Belle-CONF-0435, hep-ex/0409049 |
| KSKSKS | not yet available | –1.26 ± 0.68 ± 0.18 | –1.26 ± 0.68 ± 0.18 | Belle-CONF-0475, hep-ex/0411056 |
| All b → s-penguin | 0.41 ± 0.07 | CL=0.10 (1.7σ) | ||
| All modes | 0.665 ± 0.033 | CL=0.0016 (3.1σ) | ||
| Direct comparison of charmonium average and s-penguin average (see comments below): CL=0.00012 (3.8σ) | ||||
| Parameter: sin(2β)/sin(2φ1) | ||||
|---|---|---|---|---|
| Experiment | Value | Ref. / Comments | ||
| ALEPH | 0.84 +0.82–1.04 ± 0.16 | PL B492 (2000) 259-274 | ||
| OPAL | 3.2 +1.8–2.0 ± 0.5 | EPJ C5 (1998) 379-388 | ||
| CDF (full Run I) | 0.79 +0.41–0.44(stat+syst) | PRD 61 (2000) 072005 | ||
| Parameter: sin(2β)/sin(2φ1) | ||||
|---|---|---|---|---|
| All charmonium | 0.726 ± 0.037 | |||
| Parameter: C=–A (if not stated otherwise) | ||||
|---|---|---|---|---|
| Mode | BABAR | Belle | Average | Ref. / Comments |
| Charmonium | |λ| = 0.950 ± 0.031 ± 0.013 |
|λ| = 1.007 ± 0.041 ± 0.033 |
0.969 ± 0.028 (0.025stat-only) CL=0.30 |
BABAR-CONF-04/38, hep-ex/0408127 (submitted to PRL) Belle-CONF-0436, hep-ex/0408111 (submitted to PRD) |
| C = 0.051 ± 0.033 ± 0.014 | C = –0.007 ± 0.041 ± 0.033 |
C = 0.031 ± 0.029
(0.025stat-only)
CL=0.30 |
||
| φK0 | 0.00 ± 0.23 ± 0.05 | –0.08 ± 0.22 ± 0.09 | –0.04 ± 0.17 CL=0.81 |
BABAR-CONF-04/033, hep-ex/0408072 Belle-CONF-0435, hep-ex/0409049 |
| η'KS | –0.21 ± 0.10 ± 0.03 | 0.19 ± 0.11 ± 0.05 | –0.04 ± 0.08 CL=0.01 (2.5σ) |
BABAR-CONF-04/040, hep-ex/0408090 Belle-CONF-0435, hep-ex/0409049 |
| f0KS | –0.24 ± 0.31 ± 0.15 | 0.39 ± 0.27 ± 0.08 | 0.14 ± 0.22 CL=0.16 (1.4σ) |
BABAR-CONF-04/019, hep-ex/0408095 Belle-CONF-0435, hep-ex/0409049 |
| π0KS | 0.06 ± 0.18 ± 0.06 | 0.12 ± 0.20 ± 0.07 | 0.09 ± 0.14 CL=0.83 |
BABAR-CONF-04/030, hep-ex/0408062 Belle-CONF-0435, hep-ex/0409049 |
| ωKS | not yet available | –0.26 ± 0.48 ± 0.15 | –0.26 ± 0.48 ± 0.15 | Belle-CONF-0435, hep-ex/0409049 |
|
K+K–KS (excluding φKS) |
0.10 ± 0.14 ± 0.06 | 0.08 ± 0.12 ± 0.07 | 0.09 ± 0.10 CL=0.92 |
BABAR-CONF-04/025, hep-ex/0408076 Belle-CONF-0435, hep-ex/0409049 |
| KSKSKS | not yet available | –0.54 ± 0.34 ± 0.08 | –0.54 ± 0.34 ± 0.08 | Belle-CONF-0475, hep-ex/0411056 |
| All b → s-penguin | 0.007 ± 0.052 | CL=0.30 | ||
| All modes | 0.025 ± 0.025 | CL=0.37 | ||
| Direct comparison of charmonium average and s-penguin average (see comments above): CL=1.00 (0.0σ) | ||||
|
Constraining CJ/ψ Ks
from ACP(B+ → J/ψ K+)
and ASL: as suggested by
Y. Nir,
one can obtain a powerful SM constraint on
|λ| = |q/p||A-bar/A| via the relations
ASL = (1–|q/p|4)/(1+|q/p|4)
and
ACP(B+ → J/ψ K+)
= (|A-bar/A|2–1)/(|A-bar/A|2+1),
where ASL denotes the CP asymmetry in semileptonic
B decays,
and ACP(B+ → J/ψ K+)
is the CP-violating charge asymmetry measured in
B+ → J/ψ K+ decays.
Averaging the ASL results from
BABAR,
Belle,
CLEO,
ALEPH and
OPAL
(using also the BABAR
measurement of |q/p| from fully reconstructed B decays),
as well as the ACP(B+ → J/ψ K+)
results from
BABAR,
Belle and
CLEO,
we find respectively
ASL = –0.0026 ± 0.0067
(see
HFAG oscillation group
for more details) and
ACP(B+ → J/ψ K+)
= –0.007 ± 0.019. This
gives
|q/p| = 1.0013 ± 0.0034 and
|A-bar/A| = 0.993 ± 0.018,
and hence
|λ|indirect = 0.994 ± 0.018, which
is C = 0.006 ± 0.018
(see right hand plot below).
Discussion: the amplitude relation between neutral and charged B → J/ψ K decays has been found by Fleischer-Mannel to hold up to negligible corrections of the order O(λ3). However, the identification of |λ|, measured through the C coefficient in B0 → J/ψ K0, with |q/p||A-bar/A| assumes ΔΓBd=0. The systematic error on C from a width difference ΔΓBd/ΓBd~0.02 has been estimated by BABAR to be 0.0009. |
| Compilation of results for –η×S ≈ sin(2β)/sin(2φ1) from charmonium and s-penguin decays: BABAR and Belle separately. |
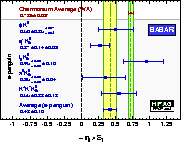 eps gif gif(high res) |
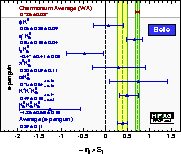 eps gif gif(high res) |
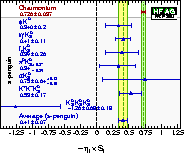
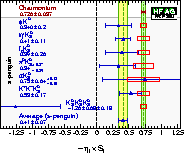
| Compilation of results for –η×S ≈ sin(2β)/sin(2φ1) from charmonium and s-penguin decays: BABAR and Belle are shown on one plot. |
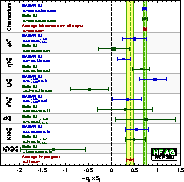 eps gif gif(high res) |
|
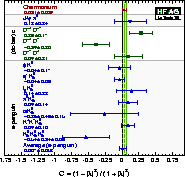
| Compilation of results for –η×S ≈ sin(2β)/sin(2φ1) and C: averages of experiments. |
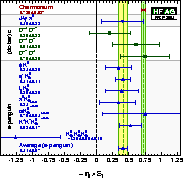 eps gif gif(high res) |
 eps gif gif(high res) |
|
Compilation of results for
–η×S ≈ sin(2β)/sin(2φ1)
from charmonium and s-penguin decays:
world averages.
The right hand plot
indicates coarse estimates of
possible theoretical uncertainties
for sin(2β)/sin(2φ1) from
the non-charmonium modes. [These estimates are obtained from dimensional arguments only, based on the CKM suppression of the Vub penguin, and on the naive contribution from tree diagrams. In general, more theoretically motivated analyses, taking advantage of the factorization property of non-leptonic B decays, obtain smaller deviations.] |
 eps gif gif(high res) |
 eps gif gif(high res) |
|
Constraining the Unitarity Triangle (ρ, η):
the measurement of sin(2β)/sin(2φ1) from charmonium modes
can be compared in the ρ-bar-η-bar plane (ρ-bar, η-bar being the
parameters in the exact (unitary)
Wolfenstein
parameterization of the CKM matrix) with the constraints from
other experimental inputs. Visit the CKMfitter and UTfit sites for results on global CKM fits using different fit techniques and input quantities. |
| Experiment | sin(2β/2φ1)J/ψK* | cos(2β/2φ1)J/ψK* | Correlation | Ref. / Comments |
|---|---|---|---|---|
|
BABAR'04 N(BB)=88m |
–0.10 ± 0.57 ± 0.14 | 3.32 +0.76–0.96 ± 0.27 | -0.37 |
BABAR-PUB-04/030, hep-ex/0411016 (submitted to PRD) |
| Belle'04 N(BB)=275m |
0.30 ± 0.32 ± 0.02 | 0.31 ± 0.91 ± 0.11
[using Solution II] |
? | Belle-CONF-0438, hep-ex/0408104 |
| Average | 0.21 ± 0.28 (CL = 0.55 → 0.6σ) |
1.69 ± 0.67 (CL = 0.026 → 2.2σ) |
? | See remark below table |
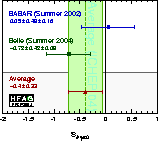
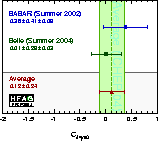
| Experiment | SJ/ψπ0 | CJ/ψπ0 = –AJ/ψπ0 | Correlation | Ref. / Comments | |
|---|---|---|---|---|---|
|
BABAR'02 N(BB)=88m |
0.05 ± 0.49 ± 0.16 | 0.38 ± 0.41 ± 0.09 | –0.12 | PRL 91 (2003) 061802 | |
| Belle'04 N(BB)=151m |
–0.72 ± 0.42 ± 0.09 | 0.01 ± 0.29 ± 0.03 | –0.12 | Belle-Preprint-2004-23, hep-ex/0408105 (submitted to PRL) | |
| Average | –0.40 ± 0.33 | 0.12 ± 0.24 | –0.12 | χ2 = 2.1 (CL=0.36 → 0.9σ) | |
 eps gif gif (high res) |
 eps gif gif (high res) |
||||
| Experiment | SD*+D*– | CD*+D*– | Correlation | Ref. / Comments |
|---|---|---|---|---|
| BABAR'03 N(BB)=88m |
Im(λ) = 0.05 ± 0.29 ± 0.10 | |λ| = 0.75 ± 0.19 ± 0.02 | 0.18 |
PRL 91 (2003) 131801 fCP-odd = 0.063 ± 0.055 ± 0.009 |
| S = 0.06 ± 0.37 ± 0.13 | C = 0.28 ± 0.23 ± 0.02 | –0.15 | ||
| Belle'04 N(BB)=152m |
–0.75 ± 0.56 ± 0.12 | 0.26 ± 0.26 ± 0.04 | –0.053 |
Belle-CONF-0453 fCP-odd = 0.19 ± 0.08 ± 0.01 |
| Average(*) | –0.20 ± 0.32 | 0.28 ± 0.17 | –0.074 | χ2 = 1.4 (CL=0.49 → 0.7σ) |
| Experiment | S+–(D*+D–) | C+–(D*+D–) | S–+(D*–D+) | C–+(D*–D+) | A(D*+–D |
Ref. / Comments |
|---|---|---|---|---|---|---|
|
BABAR'03 N(BB)=88m |
–0.82 ± 0.75 ± 0.14 | –0.47 ± 0.40 ± 0.12 | –0.24 ± 0.69 ± 0.12 | –0.22 ± 0.37 ± 0.10 | –0.03 ± 0.11 ± 0.05 | PRL 90 (2003) 221801 |
|
Belle'04 N(BB)=152m (combined fully and partially rec. B decays) |
–0.55 ± 0.39 ± 0.12 | –0.37 ± 0.22 ± 0.06 | –0.96 ± 0.43 ± 0.12 | 0.23 ± 0.25 ± 0.06 | 0.07 ± 0.08 ± 0.04 | PRL 93 (2004) 201802 |
| Average | –0.61 ± 0.36 | –0.39 ± 0.20 | –0.75 ± 0.38 | 0.09 ± 0.21 | 0.03 ± 0.07 |
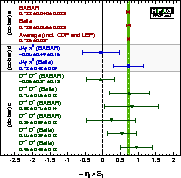
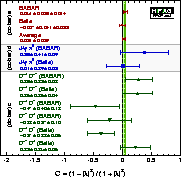
| Compilation of results for sin(2βeff/φ1,eff)=–S (left figure) and C (right figure) from time-dependent b → cc-bar d analyses. The results are compared to the values from the corresponding charmonium averages. |
 eps gif gif(high res) |
 eps gif gif(high res) |
| Experiment | SKsπ0γ | CKsπ0γ = –AKsπ0γ | Correlation | Ref. / Comments |
|---|---|---|---|---|
|
BABAR'04 N(BB)=124m |
0.25 ± 0.63 ± 0.14 | –0.57 ± 0.32 ± 0.09 | –0.01 | PRL 93 (2004) 201801 |
| Belle'04 N(BB)=275m |
–0.58 +0.46–0.38 ± 0.11 | –0.03 ± 0.34 ± 0.11 | 0.02 | Belle-CONF-0475, hep-ex/0411056 |
| Average | –0.29 ± 0.38 | –0.32 ± 0.24 | 0.01 | χ2 = 2.3 (CL=0.31 → 1.0σ) |
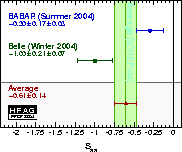
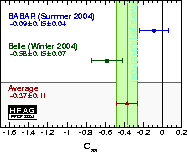
| Experiment | Sππ | Cππ = –Aππ | Correlation | Ref. / Comments | |
|---|---|---|---|---|---|
| BABAR'04 N(BB)=227m |
–0.30 ± 0.17 ± 0.03 | –0.09 ± 0.15 ± 0.04 | –0.016 | BABAR-CONF-04/047, hep-ex/0408089 | |
|
Belle'04 N(BB)=152m |
–1.00 ± 0.21 ± 0.07 | –0.58 ± 0.15 ± 0.07 | –0.286 | PRL 93 (2004) 021601 | |
| Average | –0.61 ± 0.14 | –0.37 ± 0.11 | –0.135 | χ2 = 13.1 (CL = 0.0014 → 3.2σ) | |
 eps gif gif (high res) |
 eps gif gif (high res) |
||||
The Penguin-to-tree ratio:
using as input the measured
Cππ and Sππ coefficients
together with the Wolfenstein parameters ρ and η from
the Global CKM fit
using standard constraints,
one can infer module and phase of the complex penguin
to tree (P/T) ratio
in Bd→ π+π–
decays within the Standard Model. Note that the definition of P/T is
convention-dependent (see, e.g.,
GroRos02).
One can choose to eliminate the charm quark in
the penguin loop using CKM unitarity, so that the amplitudes are
parameterized as follows:
| ||||||||
| Experiment | ACP(ρπ) | Sρπ | Cρπ | ΔSρπ | ΔCρπ | Correlations | Ref. / Comments | |
|---|---|---|---|---|---|---|---|---|
| BABAR'04 N(BB)=213m |
–0.088 ± 0.049 ± 0.013 | –0.10 ± 0.14 ± 0.04 | 0.34 ± 0.11 ± 0.05 | 0.22 ± 0.15 ± 0.03 | 0.15 ± 0.11 ± 0.03 | Table | BABAR-CONF-04/038, hep-ex/0408099 | |
| Belle'04 N(BB)=152m |
–0.16 ± 0.10 ± 0.02 | –0.28 ± 0.23 +0.10–0.08 | 0.25 ± 0.17 +0.02–0.06 | –0.30 ± 0.24 ± 0.09 | 0.38 ± 0.18 +0.02–0.04 | Table | Belle-Preprint 2004-21, hep-ex/0408003 (submitted to PRL) | |
| Average | –0.102 ± 0.045 | –0.13 ± 0.13 | 0.31 ± 0.10 | 0.09 ± 0.13 | 0.22 ± 0.10 | Table | ||
| Significance of CPV in the decay: Δχ2 = χ2(Acp=C=0) – χ2 = 14.5 (CL = 0.00070, that is: 3.4σ) | ||||||||
|
CP violation in the decay: as shown by
Charles
it is convenient to transform the experimentally motivated
CP parameters ACP(ρπ) and Cρπ
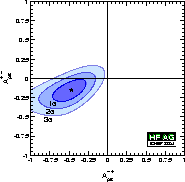
into the physically motivated ones A+–(ρπ) = (|κ+–|2–1)/(|κ+–|2+1) = –(ACP(ρπ)+Cρπ+ACP(ρπ)ΔCρπ)/(1+ΔCρπ + ACP(ρπ)Cρπ), A–+(ρπ) = (|κ–+|2–1)/(|κ–+|2+1) = (–ACP(ρπ)+Cρπ+ACP(ρπ)ΔCρπ)/(–1+ΔCρπ + ACP(ρπ)Cρπ), where κ+–=(q/p)Abar–+/A+– and κ–+=(q/p)Abar+–/A–+. With this definition A–+(ρπ) (A+–(ρπ)) describes CP violation in Bd decays where the ρ is emitted (not emitted) by the spectator interaction. Taking into account experimental correlations, one finds A+–(ρπ) = –0.15 ± 0.09, A–+(ρπ) = –0.47 +0.13–0.14. The two quantities have a linear correlation coefficient of +59%. See right hand plot for a confidence level representation in the A+–(ρπ) versus A–+(ρπ) plane. |
 eps gif gif (high res) |
||||||||||||||||||||
Flavor-charge specific branching fractions: the charge and
flavor asymmetry parameters ACP(ρπ), Cρπ and
ΔCρπ can be used to derive flavor-charge specific
rates from the
HFAG branching fraction
BR(Bd→ ρ+–π–+)=(24.0 ± 2.5)×10–6.
|
|||||||||||||||||||||
| Experiment | α/φ2 (deg) | δ+– (deg) | Ref. / Comments | ||||
|---|---|---|---|---|---|---|---|
| BABAR'04 N(BB)=213m |
113 +27–17 ± 6 | –67 +28–31 ± 7 | BABAR-CONF-04/038, hep-ex/0408099 | ||||
| Belle | not yet available | ||||||
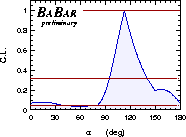
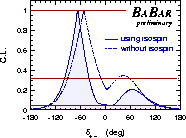
| Confidence levels for α (left hand plot) and δ+– (right hand plot) as found by BABAR |
 eps gif gif (high res) |
 eps gif gif (high res) |
|||||
| Experiment | Sρρ,long | Cρρ,long | Correlation | Ref. / Comments |
|---|---|---|---|---|
| BABAR'04 N(BB)=123m |
–0.19 ± 0.33 ± 0.11 | –0.23 ± 0.24 ± 0.14 | 0.04 |
BABAR-PROC-04-012, hep-ex/0407051 see also updated ICHEP'04 presentation |
| Belle | not yet available | |||
| The Penguin-to-tree ratio: using as input the measured Cρρ,long and Sρρ,long coefficients together with the Wolfenstein parameters ρ and η using standard constraints, one can infer module and phase of the complex penguin to tree (P/T) ratio as done in the ππ case. Plots for confidence level representations of the P/T phase versus its module can be found on the corresponding CKMfitter and UTfit pages. |
| Constraining α: using as input the measured Cρρ,long and Sρρ,long coefficients together with the present (HFAG) ρρ branching fractions and longitudinal polarization fractions (including the limit on ρ0ρ0, for which the polarization is unknown), one can perform the Gronau-London isospin analysis (electroweak penguins can be taken into account, while other SU(2)-breaking effects are usually neglected). Plots for confidence level representations of the P/T phase versus its module can be found on the corresponding CKMfitter and UTfit pages. |
| Combined α constraint from b → uu-bar d transitions: averaging the confidence level curves from the ππ and ρρ isospin analyses as well as the ρπ Dalitz plot analysis, leads to a the combined constraint: α = (100 +9 –10[1σ] +29–20[2σ]) deg, where the first errors given are at one and the second at two standard deviations, respectively. The isospin analyses are performed following the statistical interpretation of the CKMfitter analysis (Rfit). It includes the Fiertz treatment of electroweak penguins for ππ and ρρ leading to a shift in α of approximately –2 deg. |
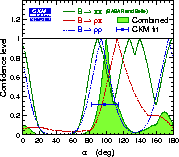 eps gif gif (high res) |
The decays Bd → D+–π–+, Bd → D*+–π–+ and Bd → D+–ρ–+ provide sensitivity to γ/φ3 because of the interference between the Cabibbo-favoured amplitude (e.g. B0 → D–π+) with the doubly Cabibbo-suppressed amplitude (e.g. B0 → D+π–). The relative weak phase between these two amplitudes is –γ/–φ3 and, when combined with the BdBd-bar mixing phase, the total phase difference is –(2β+γ)/–(2φ1+φ3).
The size of the CP violating effect in each mode depends on the ratio of magnitudes of the suppressed and favoured amplitudes, e.g., rDπ = |A(B0 → D+π–)/A(B0 → D–π+)|. Each of the ratios rDπ, rD*π and rDρ is expected to be about 0.02, and can be obtained experimentally from the corresponding suppressed charged B decays, (e.g., B+ → D+π0) using isospin, or from self-tagging decays with strangeness (e.g., B0 → Ds+π–), using SU(3). In the latter case, the theoretical uncertainties are hard to quantify. The smallness of the r values makes direct extractions from, e.g., the D+–π–+ system very difficult.
Both BABAR and Belle exploit partial reconstructions of D*+–π–+ to increase the available statistics. Both experiments also reconstruct D+–π–+ and D*+–π–+ fully, and BABAR includes the mode D+–ρ–+. Additional states with similar quark content are also possible, but for vector-vector final states an angular analysis is required, while states containing higher resonances may suffer from uncertainties due to nonresonant or other contributions.
BABAR and Belle use different observables:
Here we convert the Belle results to express them in terms of a and c. Explicitly, the conversion reads:
| Belle D*π (partial reconstruction): | aπ* = – (S+ + S–)/2 |
| cπ* = – (S+ – S–)/2 | |
| Belle D*π (full reconstruction): | aπ* = + ( 2 RD*π sin( 2φ1+φ3 + δD*π ) + 2 RD*π sin( 2φ1+φ3 – δD*π ) )/2 |
| cπ* = + ( 2 RD*π sin( 2φ1+φ3 + δD*π ) – 2 RD*π sin( 2φ1+φ3 – δD*π ) )/2 | |
| Belle Dπ (full reconstruction): | aπ = – ( 2 RDπ sin( 2φ1+φ3 + δDπ ) + 2 RDπ sin( 2φ1+φ3 – δDπ ) )/2 |
| cπ = – ( 2 RDπ sin( 2φ1+φ3 + δDπ ) – 2 RDπ sin( 2φ1+φ3 – δDπ ) )/2 |
At present we do not rescale the results to a
common set of input parameters. Also, common systematic errors
are not considered.
| Observable | BABAR | Belle | Average(*) | Ref. / Comments | ||
|---|---|---|---|---|---|---|
| partially reconstructed N(BB)=178m |
fully reconstructed N(BB)=110m |
partially reconstructed N(BB)=152m |
fully reconstructed N(BB)=152m |
|||
| aπ* | –0.041 ± 0.016 ± 0.010 | –0.049 ± 0.031 ± 0.020 | –0.031 ± 0.028 ± 0.018 | 0.060 ± 0.040 ± 0.019 | –0.030 ± 0.014
(CL=0.19) |
BABAR-CONF-04/018, hep-ex/0408038 (partially reco.) BABAR-CONF-04/029, hep-ex/0408059 (fully reco.) Belle-CONF-0448, hep-ex/0408106 (partially reco.) Belle: PRL 93 (2004) 031802; Erratum-ibid. 93 (2004) 059901 |
| cπ* | –0.015 ± 0.036 ± 0.019
(lepton tags only) |
0.044 ± 0.054 ± 0.033
(lepton tags only) |
–0.004 ± 0.028 ± 0.018 | 0.049 ± 0.040 ± 0.019 | 0.010 ± 0.021
(CL=0.66) |
|
| aπ | - | –0.032 ± 0.031 ± 0.020 | - | –0.062 ± 0.037 ± 0.018 | –0.045 ± 0.027
(CL=0.59) |
|
| cπ | - | –0.059 ± 0.055 ± 0.033
(lepton tags only) |
- | –0.025 ± 0.037 ± 0.018 | –0.035 ± 0.035
(CL=0.66) |
|
| aρ | - | –0.005 ± 0.044 ± 0.021 | - | - | –0.005 ± 0.049 | |
| cρ | - | –0.147 ± 0.074 ± 0.035
(lepton tags only) |
- | - | –0.147 ± 0.082 | |
| Compilation of the above results. |
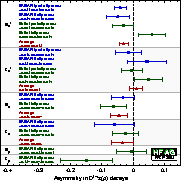 eps gif gif(high res) |
| ACP+– = [Γ(B– → D(*)CP+–K(*)– – Γ(B+ → D(*)CP+–K(*)+] / Sum , |
| RCP+– = [Γ(B– → D(*)CP+–K(*)– + Γ(B+ → D(*)CP+–K(*)+] / [Γ(B– → D(*)0 K(*)– + Γ(B+ → D(*)0-bar K(*)+]. |
| Mode | Experiment | ACP+ | ACP– | RCP+ | RCP– | Ref. / Comments |
|---|---|---|---|---|---|---|
| DCPK– | BABAR'04 N(BB)=214m |
0.40 ± 0.15 ± 0.08 | 0.21 ± 0.17 ± 0.07 | 0.87 ± 0.14 ± 0.06 | 0.80 ± 0.14 ± 0.08 | BABAR-CONF-04/039, hep-ex/0408082 |
| Belle'04 N(BB)=274m |
0.07 ± 0.14 ± 0.06 | –0.11 ± 0.14 ± 0.05 | 0.98 ± 0.18 ± 0.10 | 1.29 ± 0.16 ± 0.08 | Belle-CONF-0443 | |
| Average |
0.22 ± 0.11 | 0.02 ± 0.12 | 0.91 ± 0.12 | 1.02 ± 0.12 | ||
| D*CPK– | BABAR'04 N(BB)=123m |
–0.02 ± 0.24 ± 0.05 | - | 1.09 ± 0.26 +0.10–0.08 | - | BABAR-CONF-04/049, hep-ex/0408060 |
| Belle'04 N(BB)=274m |
–0.27 ± 0.25 ± 0.04 | 0.26 ± 0.26 ± 0.03 | 1.43 ± 0.28 ± 0.06 | 0.94 ± 0.28 ± 0.06 | Belle-CONF-0443 | |
| Average |
–0.14 ± 0.18 | 0.26 ± 0.26 | 1.25 ± 0.20 | 0.94 ± 0.29 | ||
| DCPK–* | BABAR'04 N(BB)=227m |
–0.09 ± 0.20 ± 0.06 | –0.33 ± 0.34 ± 0.10 –0.06(*) | 1.77 ± 0.37 ± 0.12 | 0.76 ± 0.29 ± 0.06 +0.04–0.14(*) | BABAR-CONF-04/012, hep-ex/0408069 |
| Belle'03 N(BB)=96m |
–0.02 ± 0.33 ± 0.07 | 0.19 ± 0.50 ± 0.04 | - | - | Belle-CONF-0316, hep-ex/0307074 | |
| Average |
–0.07 ± 0.18 | –0.16 ± 0.29 | 1.77 ± 0.39 | 0.76 ± +0.30–0.33 | ||
| AKπ = [Γ(B– → [K+π–]D(*)K(*)– – Γ(B+ → [K–π+]D(*)K(*)+] / [Γ(B– → [K+π–]D(*)K(*)– + Γ(B+ → [K–π+]D(*)K(*)+] , |
| RKπ = [Γ(B– → [K+π–]D(*)K(*)– + Γ(B+ → [K–π+]D(*)K(*)+] / [Γ(B– → [K–π+]D(*)K(*)– + Γ(B+ → [K+π–]D(*)K(*)+] . |
| Mode | Experiment | AKπ | RKπ | Ref. / Comments | |
|---|---|---|---|---|---|
|
DK–
D→Kπ |
BABAR'04 N(BB)=227m |
- | 0.013 +0.011–0.009 | BABAR-CONF-04/13, hep-ex/0408028 | |
| Belle'04 N(BB)=274m |
0.49 +0.53–0.46 ± 0.06 | 0.028 +0.015–0.014 ± 0.010 | Belle-CONF-0444, hep-ex/0408129 | ||
| Average |
0.49 +0.53–0.46 | 0.017 ± 0.009 | |||
|
D*K–
D* → Dπ0 D→Kπ |
BABAR'04 N(BB)=227m |
- | -0.001+0.010–0.006 | BABAR-CONF-04/13, hep-ex/0408028 | |
| Average |
- | -0.001+0.010–0.006 | |||
|
D*K–
D* → Dγ D→Kπ |
BABAR'04 N(BB)=227m |
- | 0.0011+0.019–0.013 | BABAR-CONF-04/13, hep-ex/0408028 | |
| Average |
- | 0.011+0.019–0.013 | |||
Constraining γ/φ3:
The rate ratios and asymmetries of the GLW and ADS methods can be
expressed in terms of amplitude ratios and strong phase differences,
as well as the weak phase difference γ/φ3.
For the GLW observables, one has:
|
| Experiment | Mode | γ/φ3 (°) | δB (°) | rB | Ref. / Comments |
|---|---|---|---|---|---|
|
Belle'04
N(BB)=274m |
DK–
D→KSπ+π– |
64 ± 19 ± 13 ± 11 | 157 ± 19 ± 11 ± 21 | 0.21 ± 0.08 ± 0.03 ± 0.04 | Belle-CONF-0476, hep-ex/0411049 |
|
D*K–
D*→Dπ0 D→KSπ+π– |
75 ± 57 ± 11 ± 11 | 321 ± 57 ± 11 ± 21 | 0.12 +0.16–0.11 ± 0.02 ± 0.04 | ||
| Combined | 68 +14–15 ± 13 ± 11 | - | - | ||
|
BABAR'04
N(BB)=227m |
DK–
D→KSπ+π– |
70 ± 44 ± 10 ± 10 | 114 ± 41 ± 8 ± 10 | < 0.19 (90% CL) | BABAR-CONF-04/043, hep-ex/0408088, |
|
D*K–
D*→Dπ0 & D*→Dγ D→KSπ+π– |
73 ± 35 ± 8 ± 10 | 303 ± 34 ± 14 ± 10 | 0.16 +0.07–0.08 ± 0.04 ± 0.02 | ||
| Combined | 70 ± 26 ± 10 ± 10 | - | - | ||
| Average | UNDER CONSTRUCTION | ||||