(home , top , next, previous)
Neutral B meson mixing: decay width differences
For both the B0 and Bs systems, the
mean decay width and the decay width difference
are defined here as
ΔΓ = ΓL - ΓH and
Γ = (ΓL + ΓH)/2,
where ΓL (ΓH)
is the decay width of the
light (heavy) mass eigenstate.
In the Standard Model, one expects ΔΓ > 0,
i.e. the light (heavy) mass eigenstate is also the short-lived
(long-lived) mass eigenstate.
In the absence of CP violation, the light (heavy) B0 or Bs mass eigenstate is
the CP-even (CP-odd) eigenstate. This assumption is made
by several analyses included in the combined results given in this section.
Combined result on the relative decay width difference in the B0 system:
|
s*ΔΓd/Γd =
0.010
±
0.037
|
from BABAR and DELPHI |
The quantity s = sign(Re(λCP)), where
λCP = (q/p)*AbarCP/ACP
refers to a CP-even final state (e.g. J/ψKLong),
is predicted to be equal to s= +1
to a high degree of confidence from the Standard Model fits
to all available contraints on the unitarity triangle.
Combined results on the decay-width difference
in the Bs system are extracted from
a global fit including all direct measurements of
ΔΓs/Γs, as well as
the lifetime measurements using Bs → J/ψ φ decays
and flavour-specific Bs decaysi, and the measurements of the
Bs → Ds(*)Ds(*)
branching fraction (CDF, D0, ALEPH and DELPHI data).
This extraction is done under the assumption of no CP violation
(see elsewhere for an extraction in presence of CP violation).
The results in the table below are shown both with and without
constraining
the quantity
(1/Γs)
× (1 + (ΔΓs/Γs)2/4)
/ (1 − (ΔΓs/Γs)2/4)
to the flavour-specific Bs lifetime average, and the
quantity 1/(2Γs/ΔΓs+1) to BR((Bs → Ds(*)Ds(*)) =
0.044
±
0.015
. In the application of the latter constraint as a Gaussian penalty function,
the theoretical uncertainty is dealt with in two ways: the PDF of the
CP-odd fraction of Bs → Ds(*)Ds(*) is taken to be a uniform
distribution ranging from 0 to 0.05 and convoluted in the Gaussian;
alternatively, the fractional uncertainty on the measured value
of the branching fraction is increased in quadrature by 30%,
and the more conservative result is taken.
The default set of results (recommended for the 2010 Review of Particle Physics)
is the one where only the constraint from τ(Bs → flavour specific)
is applied.
Fit results from CDF, D0,
ALEPH and DELPHI data |
without constraint from
τ(Bs → flavour specific)
nor BR(Bs → Ds(*)Ds(*)) |
with constraint from
τ(Bs → flavour specific)
only |
with constraint from
τ(Bs → flavour specific)
and BR(Bs → Ds(*)Ds(*)) |
| 1/Γs |
1.515
+0.034
−0.034
ps
|
1.472
+0.024
−0.026
ps
|
1.472
±
0.024
ps
|
| τShort = 1/ΓL |
1.407
+0.035
−0.034
ps
|
1.408
+0.033
−0.030
ps
|
1.408
+0.028
−0.027
ps
|
| τLong = 1/ΓH |
1.642
+0.091
+0.083
ps
|
1.543
+0.058
+0.060
ps
|
1.544
±
0.041
ps
|
| ΔΓs (95% CL range) |
[
+0.016
;
+0.192
] ps−1
|
[
−0.013
;
+0.130
] ps−1
|
[
+0.018
;
+0.102
] ps−1
|
| ΔΓs |
+0.102
+0.043
−0.043
ps−1
|
+0.062
+0.034
−0.037
ps−1
|
+0.063
±
0.022
ps−1
|
| ΔΓs/Γs (95% CL range) |
[
+0.024
;
+0.290
]
|
[
−0.020
;
+0.193
]
|
[
+0.027
;
+0.155
]
|
| ΔΓs/Γs |
+0.154
+0.067
−0.065
|
+0.092
+0.051
−0.054
|
+0.092
+0.032
−0.033
|
The left plot below shows
contours of Δ(log(L)) = 0.5
(39% CL for the enclosed 2-dim regions, 68% CL for the bands)
in the plane (1/Γs, ΔΓs) for
the average of all direct measurements (red),
the constraint given by the Bs lifetime using flavour-specific
final states (blue),
and their combination (black).
The yellow band is a theory prediction ΔΓs = 0.088 ±0.017 ps−1
which assumes no new physics in Bs mixing
[A. Lenz and U. Nierste, JHEP 06 (2007) 072].
The right plot below shows the same contours in the plane
(1/ΓL, 1/ΓH).
In both cases, the blue band represents the average
1.417
±
0.044
ps which includes all lifetime measurements with flavour-specific Bs decays,
except those which are not independent of the direct measurements used in the
ΔΓs averaging.
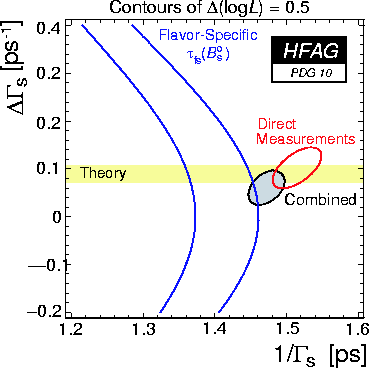
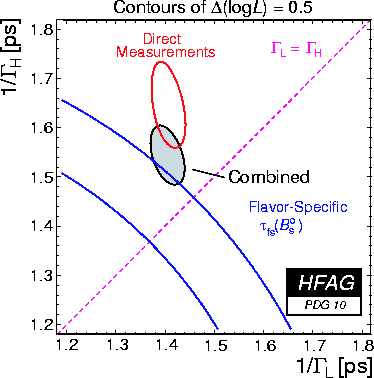
Above plots: (1/Γs, ΔΓs) gif /
(1/ΓL, 1/ΓH) gif /
(1/Γs, ΔΓs) eps /
(1/ΓL, 1/ΓH) eps /
Another (1/Γs, ΔΓs) plot
showing only the direct measurements and their average:
gif / eps /
The two plots below are similar to the plots above, but represent the combined results when including the additional
contraint from
BR((Bs → Ds(*)Ds(*)) = (
0.044
±
0.015
) × (1 ± 0.3(theory)), shown as a green band.


Above plots: (1/Γs, ΔΓs) gif /
(1/ΓL, 1/ΓH) gif /
(1/Γs, ΔΓs) eps /
(1/ΓL, 1/ΓH) eps /
(home , top , next, previous)
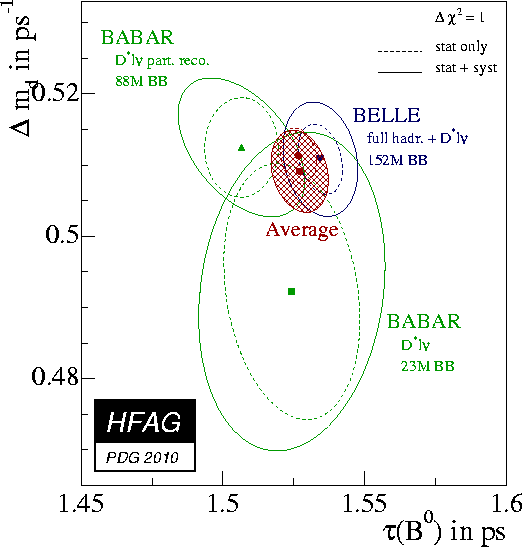
B0 mixing: oscillations and mass difference
Combined result on B0 mixing, obtained separately from time-dependent measurements of the
oscillation frequency Δmd (at high energy colliders and asymmetric B factories) and from time-integrated measurements of the
mixing probability χd at symmetric Υ(4S) machines:
| Δmd =
0.508
±
0.005
ps−1
|
from time-dependent measurements at
ALEPH, DELPHI, L3, OPAL,
CDF, D0,
BABAR, BELLE
|
| χd =
0.182
±
0.015
|
from time-integrated measurements at ARGUS and CLEO |
Assuming no CP violation in the mixing and no width difference in the
B0 system, and assuming a B0 lifetime of
1.525
±
0.009
ps (the experimental average listed above),
all above measurements
can be combined to yield the following world averages:
Δmd =
0.507
±
0.005
ps−1
xd =
0.774
±
0.008
χd =
0.1873
±
0.0024
|
from all
ALEPH, DELPHI, L3, OPAL,
CDF, D0,
BABAR, BELLE,
ARGUS and CLEO measurements |
In the plot below,
all individual measurements are listed as quoted by the experiments;
they might assume different physics inputs. The averages (which take
into account all known correlations) are quoted
after adjusting all the individual measurements to the common set of physics
inputs. The χd average from ARGUS and CLEO is converted to a Δmd measurement
assuming no CP violation, no width difference in the B0 system and a
B0 lifetime of
1.525
±
0.009
ps.
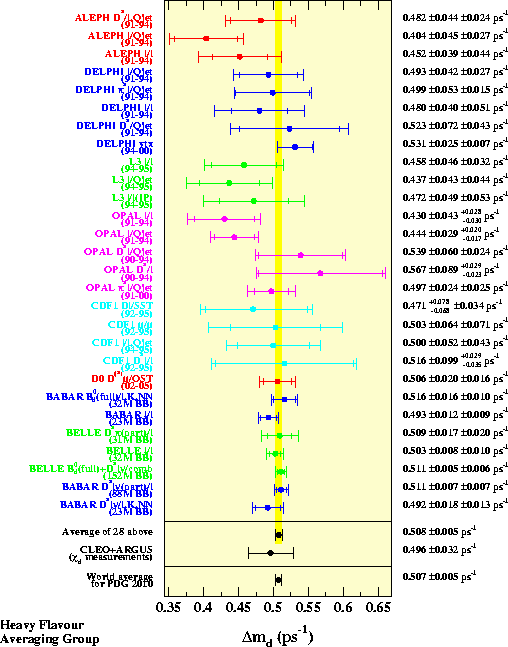
colour gif /
colour eps /
black-and-white eps /
Same without average including time-integrated (χd) measurements:
colour eps /
black-and-white eps /
Only measurements and average at LEP and CDF1:
colour eps /
black-and-white eps /
Only measurements and average at LEP:
colour eps /
black-and-white eps /
Only measurements and average at asymmetric B factories:
colour eps /
black-and-white eps /
In the plot below,
all individual experiment averages are listed as quoted by the experiments
(or computed by the working group without performing any adjustments);
they might assume different physics inputs. The global averages are quoted
after adjusting all the individual measurements to the common set of physics
inputs. The χd average from ARGUS and CLEO is converted to a Δmd measurement
assuming no CP violation, no width difference in the B0 system and a
B0 lifetime of
1.525
±
0.009
ps.
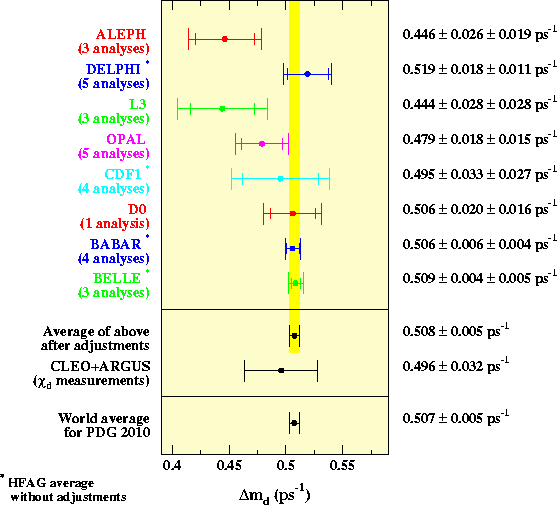
colour gif /
colour eps /
black-and-white eps /
(home , top , next, previous)
Neutral B meson mixing: CP violation
Several different parameters can be used to describe CP violation in B mixing:
|q/p|, the so-called dilepton asymetry ASL,
and the real part of εB. The
relations between these parameters are as follows
(all are exact except the last one which is an approximation valid for
small CP violation):
ASL = (|p/q|2−|q/p|2)/(|p/q|2+|q/p|2)
= (1 − |q/p|4)/(1+|q/p|4)
|q/p| = [(1−ASL)/(1+ASL)]**0.25
εB = (p−q)/(p+q)
q/p = (1−εB)/(1+εB)
ASL ~ 4 Re(εB)/(1+|εB|2)
The parameters |q/p|, ASL and Re(εB)/(1+|εB|2) are thus equivalent.
There is CP violation in the mixing
if |q/p| is different from 1, i.e. ASL is different from 0.
Averages are given below separately for the B0 and the Bs systems.
Two sets of averages are given for the B0 system in the first table:
a first set using only measurements performed at Υ(4S) machines,
and a second set using all measurements
(including those performed at high energy, but under the assumption of
no CP violation in Bs mixing). The second table presents an average for the
Bs system, based on measurements performed at the Tevatron, where some analyses
measure a mixture of the B0 and Bs parameters: the effect from the Bs is
then isolated by using the value and error of the B0 parameter
obtained at the B factories.
| CP violation parameter in B0 mixing |
|q/p| =
1.0002
±
0.0028
ASL =
−0.0005
±
0.0056
Re(εB)/(1+|εB|2) =
−0.0001
±
0.0014
|
from measurements at CLEO, BABAR and BELLE |
|q/p| =
1.0025
±
0.0019
ASL =
−0.0049
±
0.0038
Re(εB)/(1+|εB|2) =
−0.0012
±
0.0010
|
same but adding measurements from ALEPH, OPAL and D0 (and assuming ASL(Bs) = 0) |
| CP violation parameter in Bs mixing |
|q/p| =
1.0018
±
0.0047
ASL =
−0.0036
±
0.0094
|
from measurements at CDF and D0
(and assuming
ASL(B0) =
−0.0005
±
0.0056
)
|
(home , top , next, previous)
Phase difference between Bs-mixing and b→ccs amplitudes
The phase difference φs = −2βs between the Bs mixing amplitude and
the b→ccs decay amplitude of the Bs meson (for example in Bs → J/ψφ)
is the equivalent of 2β for the B0 meson.
In the Standard Model βs =
arg(−(Vts Vtb*)/(Vcs Vcb*)) ~ 1 degree.
CDF and D0 have published results on this CP-violating parameter. Combined
2D fits of βs and DGs, without external assumption,
yield two symmetric solutions
related through βs ↔ π/2−βs (or φs ↔ π−φs)
and ΔΓs ↔ −ΔΓs. Alternatively, the 2D fit is repeated, but using
external constraints provided by the flavour-specific Bs lifetime,
τ(Bs → flavour-specific) =
(1/Γs)[1+((ΔΓs/(2Γs))2]/
[1−((ΔΓs/(2Γs))2] =
1.417
±
0.042
ps
and by the semileptonic asymmetry,
ASL(Bs) = Im(Γ12/M12) =
−0.0036
±
0.0094
.
The latter is sensitive to the angle arg(−Γ12/M12),
which is predicted to be very small in the Standard Model.
A new physics phase in Bs mixing would affect
arg(−Γ12/M12) and −2βs
in the same manner. The constrained fit is performed under
the assumption that this new physics contribution is much larger than
both the Standard Model values of arg(−Γ12/M12)
and βs.
Fit results from
CDF and D0 data |
without external
constraints
|
with constraint from
τ(Bs → flavour specific)
and ASL(Bs) |
| βs |
+0.39
+0.18
−0.14
or
+1.18
+0.14
−0.18
|
+0.47
+0.13
−0.21
or
+1.09
+0.21
−0.13
|
| βs (90% CL range) |
[
+0.14
;
+0.73
]
∪
[
+0.82
;
+1.43
]
|
[
+0.10
;
+0.68
]
∪
[
+0.89
;
+1.47
]
|
| φs = −2 βs |
−0.77
+0.29
−0.37
or
−2.36
+0.37
−0.29
|
−0.94
+0.43
−0.25
or
−2.19
+0.25
−0.43
|
| φs = −2 βs (90% CL range) |
[
−1.47
;
−0.29
]
∪
[
−2.85
;
−1.65
]
|
[
−1.35
;
−0.20
]
∪
[
−2.94
;
−1.77
]
|
| ΔΓs |
+0.154
+0.054
−0.070
or
−0.154
+0.070
−0.054
ps−1
|
+0.098
+0.075
−0.026
or
−0.098
+0.026
−0.075
ps−1
|
| ΔΓs (90% CL range) |
[
+0.036
;
+0.264
] ∪
[
−0.264
;
−0.036
] ps−1
|
[
−0.163
;
+0.163
] ps−1
|
The two plot below shows different confidence-level contours in the (φs=−2βs, ΔΓs) plane,
with and without the two external constraints.
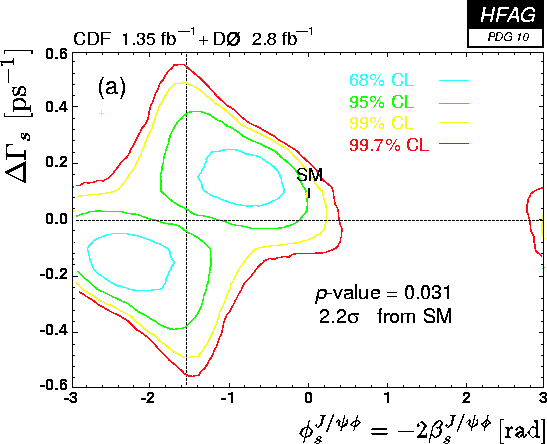
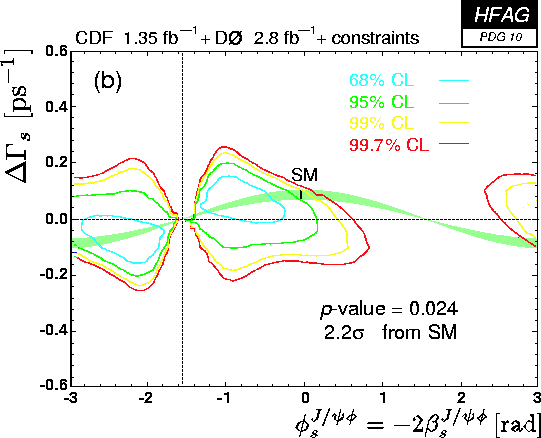
Above combined plots:
without constraint (gif,pdf,eps) /
with both contraints (gif,pdf,eps)
Individual plots (without external constraint):
CDF (gif,pdf,eps) /
D0 (gif,pdf,eps)