
Fermi LAT Performance (archived: Pass6_V11) |
Note: the most up-to-date LAT public performance page is here.
This page summarizes the top-level performance descriptions of the Fermi-LAT observatory that are currently used by the collaboration for science analysis and are available to the general public.
The LAT performance is governed primarily by three things:
- LAT hardware design
- Event reconstruction algorithms
- Background selections and event quality selections
A result of the analysis is the production of full Instrument Response Functions (IRFs), describing the performance as a function of photon energy, incidence angle, conversion point within the instrument, and other important parameters.
Pass6_V11 Instrument Response Functions
The plots below represent the work of many people in the LAT team. They correspond to the status of the analysis known as Pass6 version 11 (also called Pass6_V11 or P6_V11), Diffuse class.
Important caveats are associated with these IRFs and should be kept in mind when performing analysis of the publicly distributed Fermi-LAT data.
Performance plots
Note: Starting from the front of the instrument, the LAT tracker (TKR) has 12 layers of 3% radiation length tungsten converters (THIN or FRONT section), followed by 4 layers of 18% r.l. tungsten converters (THICK or BACK section). These sections have intrinsically different PSF due to multiple scattering, and the performance plots are presented for both of these sections.
Note: the following plots are produced via the interface to the tabulated IRF values used internally by the LAT science tools. When plotted versus the energy of the incident photons, the response functions are sampled in 5 points per energy decade, which are clearly indicated on the plots and smoothly connected for graphical clarity. Similarly, suitable sets of sampling points are used for plotting specific IRFs vs. theta or phi. As a consequence, we warn against using the values derived from the figures below for any numerical evaluation of the LAT performance.
Effective Area
The plots below are:
- the effective area as a function of energy for normal incidence photons (specifically photons impinging on the instrument at cos(theta) > 0.975);
- the effective area as a function of incidence angle theta for 10 GeV photons;
- the effective area as a function of the azimuthal angle phi for 10 GeV photons, 30 degrees off-axis;
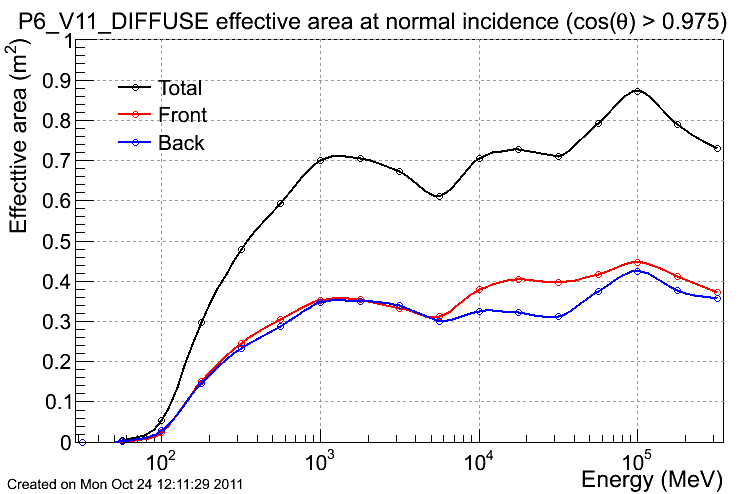
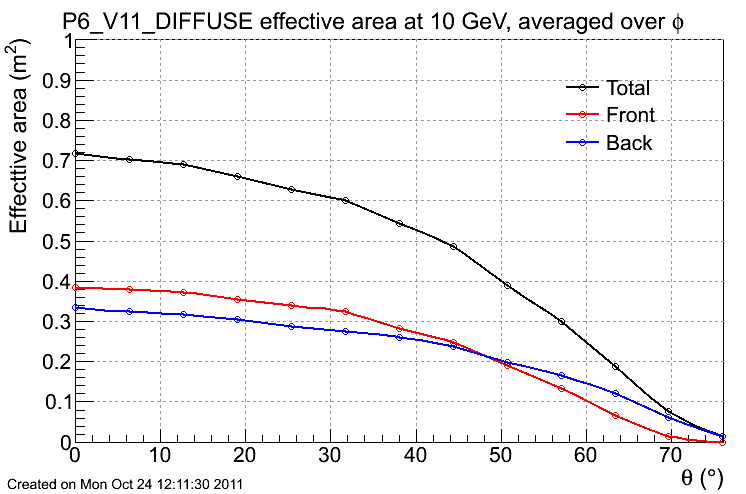
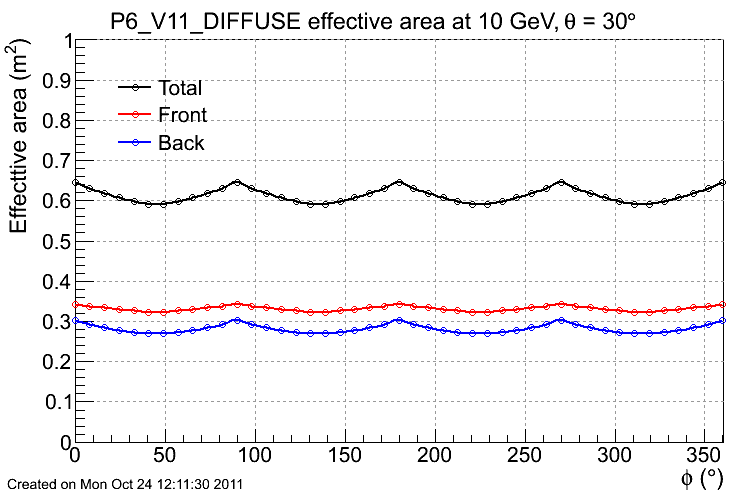
Acceptance
Defined here as the effective area integrated over the solid angle. Notice that the acceptance has a slower turn-on wrt the effective area, highlighting the dependence of the FOV on energy. That is the intrinsic acceptance regardless of the orbital characteristics. To obtain the effective acceptance, the curve has to be scaled by a constant factor which takes into account the instrument deadtime; the South Atlantic Anomaly (SAA), where the LAT does not take data; and details of the observation strategy (about 20% for standard survey and according to current simulations).
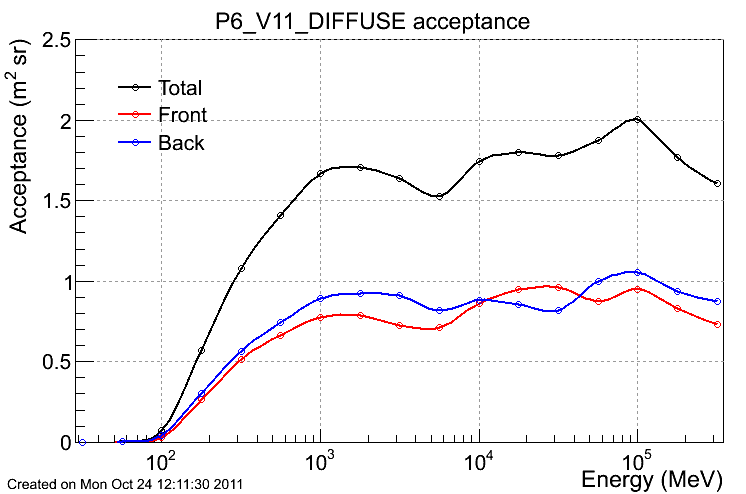
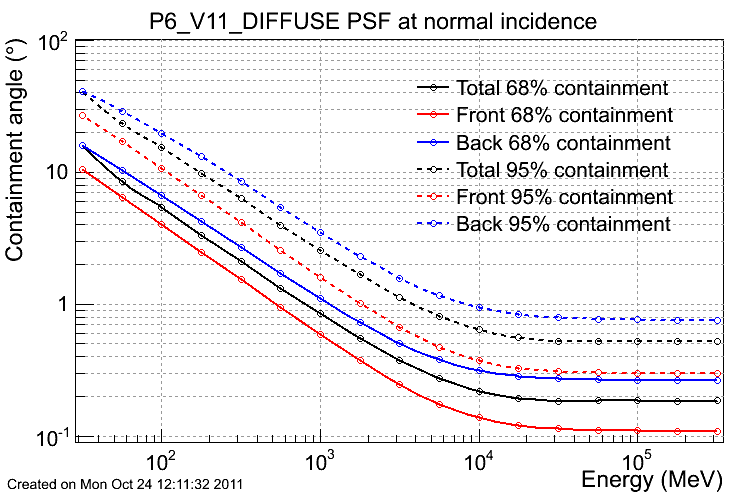
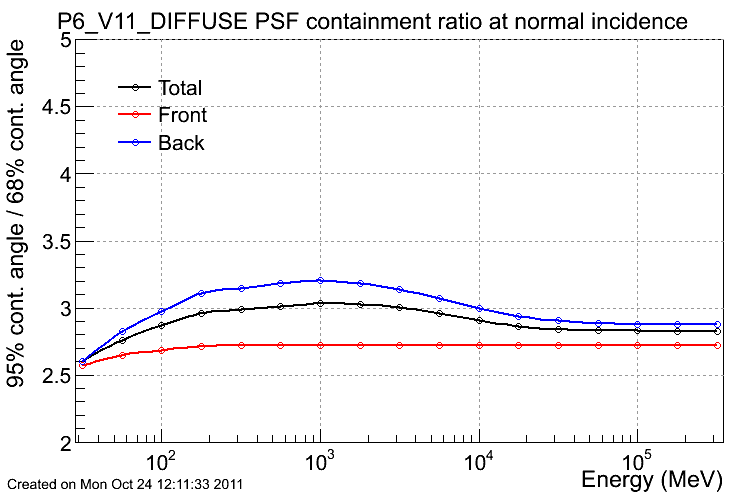
Point Spread Function (PSF)
In the P7_V6 response functions (with the exception of the P7TRANSIENT_V6 event class) the PSF is derived from flight data and, unlike the P6_V3 series, does not include any dependence on the off-axis angle.
The plots below are:
- 68% and 95% containment angles of the reconstructed incoming photon direction for normal incidence photons;
- the ratio PSF95% / PSF68%, which is a useful indicator of the magnitude of the tails of the distribution.
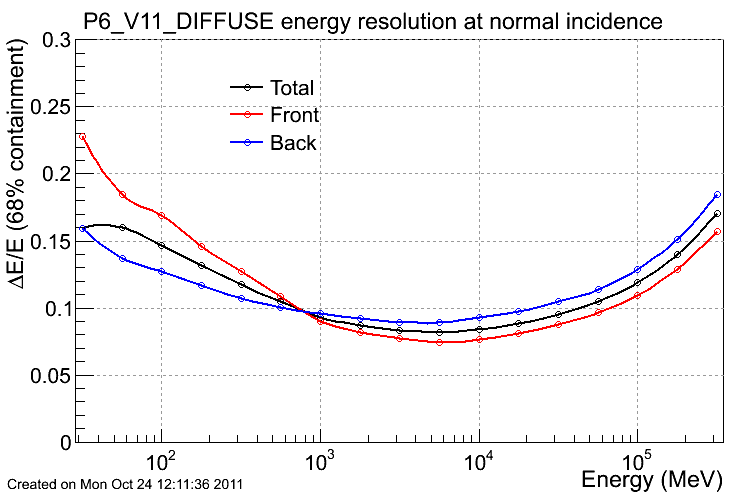
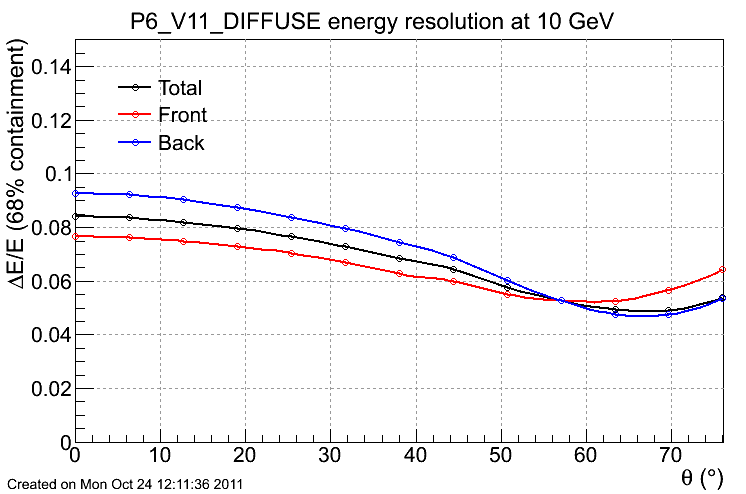
Energy resolution
The plots below are:
- energy resolution (i.e. 68% containment of the reconstructed incoming photon energy) as a function of energy for normal incident photons;
- energy resolution as a function of incidence angle for 10 GeV photons.
Science performance requirements for the LAT are given in Table 1 of the Science Requirements Document.
The Fermi data and the full set of response functions and Science Analysis Tools can be downloaded from the Fermi Science Support Center website's Data Section.
Useful links:
- LAT Home Page
- LAT Design, Development, and Operations Page
- Fermi Mission
- Fermi Science Support Center
- Fermi Users Group
- GBM Home Page
Updated on October 27, 2011, maintained by Riccardo Rando (riccardo.rando@pd.infn.it), Eric Charles (echarles@slac.stanford.edu), Seth Digel (digel@slac.stanford.edu) and Luca Baldini (luca.baldini@pi.infn.it).